個別数学系専門塾
学習塾
インフィニティ
高校生・受験生・
大学生・社会人対象
偽コインの問題【入門編】~問題
コインが3枚と天秤があります.3枚のコインのうち,1枚は偽物で本物よりも若干軽くできています.天秤を1度だけ使って偽コインを見つけて下さい .
偽コインの問題【入門編】~解答
コインを左右の皿に1枚ずつのせます.
天秤が傾けば上に上がった皿にのっているコインが偽物です.
もし,傾かなければ,天秤にのせなかったコインが偽物です.
偽コインの問題【基礎編】~問題
コインが27枚と天秤があります.27枚のコインのうち,1枚は偽物で本物よりも若干軽くできています.天秤を3度だけ使って偽コインを見つけて下さい.
偽コインの問題【基礎編】~解答
コインを左右の皿に9枚ずつのせます.
天秤が傾けば上に上がった皿にのっている9枚のコインのいずれかが偽物です.
天秤が傾かなければ,天秤にのせなかった9枚のコインの中に偽物があります.
ここで,偽物のコインは9枚の中のいずれかに絞られました.
次はその9枚の中から6枚を選び出し,3枚ずつ左右の皿にのせます.
さっきと同様に,天秤が傾けば上になった皿にのっている3枚のうちのいずれかが偽物です.
つりあえば,残った3枚の中に偽物があります.
これで,偽物のコインは3枚のうちのいずれかに絞られました.
この先は「偽コインの問題【入門編】」の解答をご覧下さい.
モンティ・ホール問題~問題
モンティ・ホール (Monty Hall) が司会を務めるアメリカのゲームショー番組、「Let's make a deal」の中で行われたゲームに関した問題です.
あなたはテレビ番組のクイズ大会で優勝しました.
商品の入った箱が目の前に三つ置かれています.
三つのうち,一つには世界一周旅行の目録が入っており,残りの二つは「はずれ」です.
三つの箱の中なら一つをあなたは選びました.
すると,司会者が残りの二つの箱のうち,一つを開けて見せました.
その箱の中は「はずれ」でした.
因みに,司会者はどの箱に世界一周旅行の目録が入っているかを知っていまし,番組を盛り上げるため賞品の入っている箱を開けることはしません.
そこで司会者はあなたにこう言いました.
「今なら,箱を選び直してもいいですよ!」
確率を考えたとき,あなたはもう一方の箱を選ぶべきでしょうか?それとも,最初に選んだ箱のままにすべきでしょうか?
モンティ・ホール問題~解答
説明のために,三つの箱にA,B,Cと名前をつけます.
三つの箱に商品が入っている確率は下表のようにそれぞれ1/3となります.
| 箱 | 確率 |
| A | 1/3 |
| B | 1/3 |
| C | 1/3 |
いま,あなたはAの箱を選んだとします.
1) 箱Aに商品が入っているとき:
司会者が開ける箱はBでもCでもよいので,それぞれを開ける確率は1/2となります.
ですから,箱Aに商品が入っていて,箱Bを開ける確率は1/3×1/2=1/6となります.同様に,箱Cを開ける確率も1/6です.
2) 箱Bに商品が入っているとき:
箱Aはあなたが選んだ箱ですし,箱Bには賞品が入っているので,司会者が開けられる箱は箱Cに限られます.なので,箱Bを開ける確率は1/3×0 = 0となり,箱Cを開ける確率は1/3×1 = 1/3です.
3) 箱Cに商品が入っているとき:
箱Aはあなたが選んだ箱ですし,箱Cには賞品が入っているので,司会者が開けられる箱は箱Bに限られます.なので,箱Bを開ける確率は1/3×1 = 1/3となり,箱Cを開ける確率は1/3×0 = 0です.
これらをまとめたものが下の表になります.
| 賞品の入っている箱 | 箱Aを開ける確率 | 箱Bを開ける確率 | 箱Cを開ける確率 |
|---|---|---|---|
| A | 0 | 1/6 | 1/6 |
| B | 0 | 0 | 1/3 |
| C | 0 | 1/3 | 0 |
箱Aに商品が入っていて,あなたが箱Aを選び,司会者が箱Bを開ける確率は1/6です.
一方,箱Cに商品が入っていて,あなたが箱Aを選び,司会者が箱Bを開ける確率は1/3です.
箱Cに商品が入っている確率は箱Aに商品が入っている確率の2倍になりますから,
「あなたはもう一方の箱を選ぶ」
というのが確率的に考えたときのよい戦略となります.
50枚の扉~問題
閉じた扉が50枚と人が50人います.
扉と人にはそれぞれ1番から50番までの番号がついています.
それぞれの人は自分の番号の整数倍の番号の扉を,開いている場合には閉め,閉まっている場合には開けます.
まず1番の人が1の倍数の扉,すなわち1番,2番,3番,・・・50番の扉を開けます.
なぜなら,最初は全ての扉が閉まっているので.
次に2番の人が2の倍数の扉,2番,4番,6番,・・・50番の扉を閉めます.1番の人が全ての扉を開けてしまいましたので,閉めるしかありません.
次に3番の人です.3番の扉は開いているので,閉めます.6番の扉は閉まっているので,開けます.というふうに順々に9番から48番までの扉を開けたり閉めたりします.
さて,問題です.50番までの人が全員,開けたり閉めたりを行った後で,開いている扉は何枚あるでしょうか?
.
50枚の扉~解答
この問題は整数の約数に関する問題です.
ある整数の約数が偶数個であれば閉じたままとなり,奇数個であれば扉は開くことになります.
具体的な例を通して考えてみましょう.
整数6の約数は1,2,3,6の四つです.この問題に当てはめると1番の人が開け,2番の人が閉め,3番の人が開けて,6番の人が閉めます.
同様に整数24の約数は 1,2,3,4,6,8,12,24です.
このように多くの整数は画数の数が偶数個です.
この問題に当てはめると「扉は閉まっている」になります.
では,約数の個数が奇数個の場合はどんな場合でしょうか. 例えば,整数4です. この場合約数は1,2,4の三つです. 他に,整数9や16などがそうです. これらの共通点は何かと考えると,いずれも,ある整数の二乗になっている数です.
結果として,50人が扉の開け閉めをした後に,空いている扉は1番,4番,9番,16番,25番,36番,49番の計7つです.
素因数分解を知っている人は,それを使ってみると,もう少し明快となります.
ビュフォンの針【実験的に円周率を求める】~問題
縫い針と大きな紙,そして定規と筆記具を準備します.
縫い針の長さが L のとき,大きな紙に幅 2L間隔で平行線を何本も引きます.
この紙に向かってデタラメに縫い針を投げたとき,縫い針が平行線と交わる(接するも含む)確率を求めて下さい.
.
ビュフォンの針【実験的に円周率を求める】~解答
まず,数式を考える前に平行線と針の関係を図を使って考えてみましょう.
図1のように様々な位置関係が考えられます.
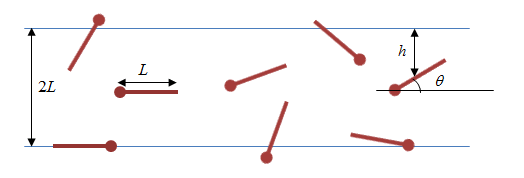
図1 平行線と針の関係
平行線と針が接するか否かは針の中心から平行線までの距離 h と針が平行線となす角 θ によって決まります.
ここで,平行線は 2L 間隔で引かれていますので,$0 \leq h \leq L$
です.
また,$0 \leq \theta \leq \pi/2 $
として考えます.
$\theta = 0$ の場合は $h = 0$ の時を除いて,交わりません.
$\theta \neq 0$ のとき,$h \leq L/2\sin \theta$
であれば交わります.
これらを図にして考えてみます.
横軸に$\theta$ ,縦軸に$h$ をとります.考えている範囲は上記のように
$0 \leq h \leq L, 0 \leq \theta \leq \pi/2$
です.
図で表すと図2の緑色の部分となります.
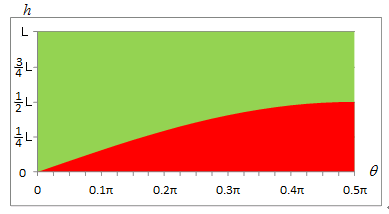
図2 針が平行線と交わる条件
針が平行線と交わるための条件は
$ h \leq L/2 \sin \theta$
ですから図2の赤色の部分が交わる範囲です.
すなわち,針が平行線と交わる確率は赤色の面積を緑色の面積で割った値となります
.
緑色の面積は Lπ/2 です.
では赤色の部分の面積を求めましょう.
赤色の部分の面積 $S$ は
\[
S = \int_0^{\pi / 2} \frac{L}{2} \sin \theta d\theta = \Bigl[ -\frac{l}{2} \cos \theta \Bigr]_0^{\pi / 2} = \frac{L}{2}
\]
により求まります.
よって,針が平行線と交わる確率は
\[
\frac{L}{2} / \frac{L \pi}{2} = \frac{1}{\pi}
\]
となります.
将棋盤とドミノ~問題
将棋盤(9×9のマス)にドミノ牌(1×2のマス)を敷き詰めることを考えます. もちろん,そのままでは将棋盤のマス全てをドミノ牌で覆い尽くすことはできません. なぜなら,将棋盤は81マスあり,ドミノ牌は2マスですから,81÷2では余りがでてしまうからです.
そこで,将棋盤から1マスだけドミノ牌を置かなくても良い場所を決めます.
そうすると将棋盤上のマスは80マスとなり2で割り切れます.
下の図のようにドミノ牌を置かない場所(図中の×印)を定めたとき,残りの80マスをドミノ牌で覆いつくすことは可能でしょうか?
 問題1
問題1
 問題2
問題2
将棋盤とドミノ~解答
問題1はドミノで埋め尽くすことはできましたが,
B 問題2はどんなにがんばっても,
ドミノで埋め尽くすことはできなかったはずです.
この違いはどこから来るのでしょうか?
まず,ドミノの半分を赤く塗ります.

将棋盤は市松模様に塗ります.

これで準備は終了です.
あとは将棋盤にぬった色に従ってドミノを配置していけばよいのです.
問題1:
問題では×印をしたマス目を今度はわかりやすいように緑色で塗りつぶしました.
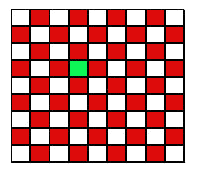
図中の赤マスと白マスの個数を数えますと,どちらも40になります.
赤マスと白マスの数が同じですから,それぞれにドミノの色を対応させればよいので,
うまく置くことができたのです.
では,問題2の場合はどうでしょうか.
問題2:
前問と同様に問題では×印をしたマス目を緑色で塗りつぶしました.
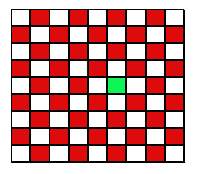
さきほどと同じく赤マスと白マスの色を数えてみましょう.
今度は赤マスが39個なのに対して,白マスは41個あります.
これは,39個のドミノを使って配置すると,最後に2マス残るものの,
その2マスはどちらも白,即ち,隣り合って,残ることはないことを示しています.
結果,問題1は埋め尽くすことをできますが,問題2は埋め尽くすことができません.
わたしは病気なのか?~問題
A国では(英国ではありません),Xという病気にかかっている人が 0.01 % いる.
もし,病気Xに感染している場合には,検査をすると陽性となる確率が99.9 %だそうだ.
感染していない場合には,検査で陰性となる可能性は 99.99 %だ.
つまり,0.01 %の人が実際には感染していないのに,陽性と判定される.
A国人のあなたはひょんなことから,この検査を受けることになり,検>査してみると陽性であった.
さて問題です.
あなたはあなた自身が病気に感染している確率は直感的にどれくらいだと思いますか?
また,直感的ではなく,数学的には何%でしょうか?
わたしは病気なのか?~解答
数学的に解く前に,あなたは直感的に感染している確率をどれくらいと思いましたか
.
おそらく,ほぼ間違いなくとか,99%, 99.9%などと思ったのではないでしょうか.
余談ですが,あるお医者さんに伺ってみたところ,「間違いなく感染しているよ」と
おっ
しゃっておりました.
さて,数学的に解いてみましょう.
この問題は条件付き確率の問題です.
条件付き確率$P_Y(X)$は,ある事象$Y$が起こる条件のもとで事象$X$が起こる確率を
いい
,
\[
P_Y(X) = \frac{P(X \cap Y)}{P(Y)}
\]
と定義されます.
(条件付き確率は$P_Y(X), P(X|Y)$といった書き方が,同時確率は$P(X\cap Y), P(X,Y)$>といった書き方がありますが,ここでは高校の教科書に出て来る記法を採用しま
す.)
この問題の場合,$Y$に相当するのは「検査の結果が陽性」,$X$に相当するのは「感
染し
ている」です.
ですから$P(X \cap Y)$は「感染していて,結果が陽性」を示しますので,問題文か>らわ>かる通り,
\[
P(X \cap Y)= \frac{1}{10000} \frac{999}{1000}
\]
です.
次に$P(Y)$を求めます.検査が陽性となるのは,感染していて陽性となる,すなわち
$P(X \cap Y)$の場合と感染していなくて陽性となる$P(\bar{X} \cap Y)$の二通りが
あります
.
$P(X \cap Y)$は上で計算しました.
$P(\bar{X} \cap Y)$は
\[
P(\bar{X} \cap Y)= \frac{9999}{10000} \frac{1}{10000}
\]
となります.
これらより,
\[
P_Y(X) = \frac{P(X \cap Y)}{P(Y)}=\frac{P(X \cap Y)}{P(X \cap Y) + P(\bar{X} \cap Y)} =
\frac{ \frac{1}{10000} \frac{999}{1000} }
{ \frac{1}{10000} \frac{999}{1000}
+ \frac{9999}{10000} \frac{1}{10000} }
\approx \frac {1}{2}
\]
となり,感染している確率は約50%となります.
チョキなしジャンケン~問題
Aさん,Bさんの二人がじゃんけんをします.
ただしチョキ(地方によってはチー)なしです.
得点は次の表に従って得られます.
| Aさん | Bさん | Aさんの得点 | Bさんの得点 |
|---|---|---|---|
| グー | グー | 0点 | 6点 |
| グー | パー | 3点 | 0点 |
| パー | グー | 3点 | 0点 |
| パー | パー | 0点 | 1点 |
どちらがどういう戦略でグーやパーを出したときに最も有利になりますか.
チョキなしジャンケン~解答
Aさんがグーを出す確率を$P(A)$, Bさんがグーを出す確率を$P(B)$とします.
したがって,Aさん,Bさんがパーを出す確率は$P(\bar{A}), P(\bar{B})$となります
.
さらに,Bさんが得点するのではなく,Aさんが減点されると考え,問題に示された表
を
| Aさん | Bさん | Aさんの得点 | Bさんの得点 |
|---|---|---|---|
| グー | グー | -6点 | 0点 |
| グー | パー | 3点 | 0点 |
| パー | グー | 3点 | 0点 |
| パー | パー | -1点 | 0点 |
のように読み替えます.
このとき,
Aさんが得る得点の期待値$E[P(A)]$は
\begin{eqnarray}
E[P(A)]& = &-6 P(A) P(B) + (-1)P(\bar{A})P(\bar{B}) \\
& + &3 P(A)P(\bar{B}) +3 P(\bar{A}) P(B) \\
& = &-6 P(A) P(B) -(1-P(A))(1-P(B))\\
& + & 3P(A)(1-P(B)) +3(1-P(A))P(B) \\
& = &-13P(A)P(B) +4P(A) +4P(B) -1 \\
& = & (4-13P(A))P(B) + 4P(A) +1
\end{eqnarray}
となります.
ここで,$4P(A)+1$は正であるため, $4-13P(A)=0$
すなわち,Aさんがグーを4/13 の確率で出した時に,
Aさんが勝つことになります.
円周率と誤差のはなし~問題
問題というよりは,おはなしに近い話題です.
円周率は無理数(より正確に言うと代数的数)です.
ですから,無限に,そして不規則に小数点以下に数が連なります.
ここでは小数点以下50桁で打ち切った円周率(以下,近似した円周率)と真の円周率の誤差はどの程度になるかを考えてみたいと思います.
地球とほぼ同じ大きさの半径6,400kmの真球の容器を考えます.
その容器に半径1mmの小球を入れ,埋め尽くします.
このとき,小球と小球の隙間は考えないこととします.
次に,その容器から小球を一つ取り出し,地球から一番近い恒星(アルファ・ケンタウリ)に一つ置きます.
この星までの距離は4.2光年です.
因みに,1光年は$9.45 \times 10^{12}$kmです.
さらに,二つ目の小球を容器から取り出し,さらに4.2光年離れた先に置きます.
これを容器が空になるまで繰り返します.
さて,ここからが問題です.
地球から最後の1個を置いた地点までを半径とした円を考えます.
この円の円周を近似した円周率を用いて測ったときと,真の円周率を用いて測ったときの誤差はどの程度になるでしょうか.
.
円周率と誤差のはなし~解答
計算をわかり易くするために,容器の半径を$R$,小球の半径を$r$>とします.
このとき,地球とほぼ同じ大きさの容器の体積$V_1$は
\[
V_1 = 4/3 \pi R^3
\]
となり,また,小球の体積$V_2$は
\[
V_2 = 4/3 \pi r^3
\]
となるので,容器に入っている小球の個数は
\[
V_1 / V_2 = R^3 / r^3
\]
となります.
さらに,恒星までの距離を$d$とおくと,考えている大きな円の半>径は
$d V_1 / V_2 $
となります.
これにメートルを単位として数値を代入すると
\[
d V_1 / V_2 = 4.2 \times 9.45 \times 10^{15} \times \left( \frac{6.4 \times 10^6}{1.0 \times 10^{-3}} \right)^3 \simeq 1 \times 10^{46}
\]
が得られます.
近似した円周率を$\hat{\pi}$とすると
\[
\pi - \hat{\pi} \leq 1.0 \times 10^{-50}
\]
ですから,円周の差は
\[
2\pi d V_1 / V_2 - 2 \hat{\pi} d V_1 /V_2 \leq 2 \times 1 \times 10^{-50} \times 10^{46} = 2.0 \times 10^{-4}
\]
となります.
すなわち,誤差は0.2ミリメートル程度となります.
円が分割する領域の数~問題
一枚の紙に一つの円を描くと内側,外側の二つの領域ができあがります.
次に二つ目の円を既に描いてある円と異なる二点で交わるように描くと四つの領域ができあがります.
三つ目以降の円も既に描いてある円全てと異なる2点で交わりかつ,既にある円同士の交点を通らないように描き続けると10個目の円を描き終えたときには幾つの領域に分割されているでしょうか.
(数研出版発行の問題集から改題)
円が分割する領域の数~解答
円を $n$ 個書いたときの領域の数を $R_n$ とします.
このとき,$R_1 = 2$ です.
既に $n$ 個の円が書いてあり,$n+1$ 個目の円書く場合を考えます.
$n+1$ 個目の円は,既に $n$ 個の円が書いてありますから,この $n+1$ 個目の円は
$n$ 個の円と交わります.
角度を変えて言うと,$2n$ 本の線と交わることになります.
つまり,今書いた $n+1$ 個目の円上には,他の円との交点が $2n$ 個並びます.
ですから,$n+1$ 個目の円を描いたことにより増えた領域は $2n$ 個です.
これを式で表しますと
\[ R_{n+1} = R_n + 2n \]
となります.
これは階差数列$S_n$の一般項が$S_n = 2n$ と表されることになりますので,
階差数列を用いて一般項を求める公式を使うと
\[ R_n = R_1 + \sum_{k=1}^{n-1} S_k \]
となります.
これを解くと
\[ S_n = n(n-1)+2 \]
が得られます.
問題では10個目の円を描き終えたときの領域の個数を問われていますので,
\[ R_{10} = 92 \]
となり,領域の個数は92個です.
正直村の浮気問題~問題
ある村に結婚した夫婦がたくさんいる.
その村の女性はよその夫が浮気をすればすぐに必ず気付くが,
自分の夫の浮気には気付かない.
この村は非常に厳格な女性上位で,自分の夫が浮気をしたと証明された場合,
女性はその日のうちに夫を殺さなければならない.
女性は皆この掟を非常に忠実に守っており,頭が良く,そして互いに頭がよいことを知っている.
一方,情け深いので,誰かの夫が浮気をしていてもそれをその妻本人には決して教えない.
さて,この村の夫たちのうち29人が浮気をしていたとする.
(つまり,自分の夫が浮気をしていない妻は浮気をしている男を29人知っており,
自分の夫が浮気をしている妻は浮気をしている男を28人知っていることになる.)
しかし,自分の夫が浮気をしていると証明できる妻はいないので,
村は毎日楽しく,そして平穏であった.
ある日,森向こうにいる族長が村にやってきた.
族長は誠実な人で,族長の言葉を村の誰もが信じていた.
族長は集まった村人全員に向かい,
「少なくとも一人浮気をしている夫がいる」
と警告した.
さて問題です.
この村ではいつか,何かが起こるでしょうか?
それとも平穏な日々が続くでしょうか?
正直村の浮気問題~解答
簡単のために,浮気をしている人数を少ないところから考えていきます.
もし,浮気をしている人が一人であるならば,族長が「少なくとも一人浮気をしている夫がいる」と言った段階でその浮気をしている夫の奥さんは誰が浮気をしているか一人も知らないので,自動的に,自分の夫が浮気をしているとわかります.ですから,翌日にはその夫はこの世からいなくなってしまうのです.
では,浮気をしている人が二人であればどうなるでしょうか.
浮気をしている人を仮に,AさんとBさんとします.Aさん,Bさんの奥さん以外はその二人を知っています.一方,Aさんの奥さんはBさんが浮気をしていることを知っており,Bさんの奥さんはAさんが浮気をしていることを知っています.ですから,この段階で,Aさんの奥さんは,『明日,Bさんはこの世からいなくなるなぁ』と思い,Bさんの奥さんは『明日,Aさんはこの世からいなくなるなぁ』と思います.
ところが,翌日,Aさんも,Bさんも生きている.ここで,Aさんの奥さんは考えます.
『もし,村の中で浮気をしている人が一人しかいないのであれば,Bさんはもう,この世にいないはず.なのに,まだ生きているということは,浮気をしている人が二人いたことになり,そのもう一人は,自分の夫だ』と気付きます.
全く同じことをBさんの奥さんも気付きます.ですから,族長が宣言した,翌々日に二人はこの世を去っているのです.
浮気をしている人が三人ですと,もう少し話が複雑になってきます.
浮気をしているのがAさん,Bさん,Cさんの三人とします.この三人の奥さん以外の人は三人とも知っていますので,以下の話には関係ありません.一方,この三人の奥さんは自分の夫以外の二人が浮気をしていることを知っています.
以下,少々複雑になりますが,Aさんの奥さんが何を考えるかを記します.
『浮気をしているのは二人,すなわちBさんとCさん.Bさんの奥さんは浮気をしているのはCさん一人だと思っているし,Cさんの奥さんも浮気をしているのがBさん一人だと思っている.だから,Bさんの奥さんは,明日Cさんの夫が世を去っていると考え,Cさんの奥さんは,明日Bさんの夫が世を去っていると考える.でも,明日になってもBさんもCさんもこの世にいることから,自分の夫が浮気をしていると明日気づき,明後日にはBさん,Cさんの両名がこの世にいない』
これがAさんの奥さんの考えです.ところが,二日後になってもBさんもCさんもこの世にいる.この段階でAさんの奥さんは自分の夫が浮気をしていることに初めて気づきます.
これと同じことをBさんの奥さんも,Cさんの奥さんも考えます.よって三日後,A,B,Cの三人はこの世を去っているのです.
この考え方をおしすすめていきますと.問題にある29人が浮気をしている場合には,
【28日後の朝までは何も起きないが,29日後には29人がこの世を去っている】
というのが答えとなります.
サイコロの目の出方~問題
確率の問題によく出てくるように,サイコロを使った話です.
サイコロを繰り返し振るとき,「1」の目が出た次に「2」の目が出るパターンを「12」と書くこととします.
さて,問題のはじまりです.サイコロを振り始めてから,初めて「123456」のパターンが出るまでのサイコロを振る回数の期待値は$6^6 = 46656$です.
では,初めてパターン「123451」や「123123」が出るまでのサイコロを振る回数の期待値をそれぞれ求めて下さい.
サイコロの目の出方~解答
求める期待値を$E[X]$ とすると,以下のような連立方程式が成立します.
\[
\left\{
\begin{array}{lcl}
E[X] & = & \frac{5}{6}\left( 1 + E[X]\right) + \frac{1}{6}\left(1+E[Y_{1}]\right) \\
E[Y_{1}] & = & \frac{1}{6}\left(1+E[Y_{1}]\right) + \frac{4}{6}\left( 1 + E[X]\right) + \frac{1}{6}\left(1+E[Y_{12}]\right) \\
E[Y_{12}] & = & \frac{1}{6}\left(1+E[Y_{1}]\right) + \frac{4}{6}\left( 1 + E[X]\right) + \frac{1}{6}\left(1+E[Y_{123}]\right) \\
E[Y_{123}] & = & \frac{1}{6}\left(1+E[Y_{1}]\right) + \frac{4}{6}\left( 1 + E[X]\right) + \frac{1}{6}\left(1+E[Y_{1234}]\right) \\
E[Y_{1234}] & = & \frac{1}{6}\left(1+E[Y_{1}]\right) + \frac{4}{6}\left( 1 + E[X]\right) + \frac{1}{6}\left(1+E[Y_{12345}]\right) \\
E[Y_{12345}] & = & \frac{5}{6}\left( 1 + E[X]\right) + \frac{1}{6} \\
\end{array}
\right.
\]
第1式より順に説明します.
第1式第一項は「1」以外の目が出た場合で,今振った分の1を加算し$(1+E[X])$ がその後の期待値となります.
因みに,5/6は「1」以外の数字が出る確率です.
一方,第2項は「1」が出た場合の計算となります.
「1」が出た上で残りの列「23451」の出る期待値を$E[Y_{1}]$ で表しています.
第2式は第1式に現れた$E[Y_{1}]$を求める式です.
第1項は次に「1」が出た場合の期待値を計算しており,また「1」が出ましたので$(1+E[Y_{1}])$ となります.
第2項は「3,4,5,6」のいずれかが出た場合を想定しており,4/6の確率でそれらが出現し,その場合,初期状態(サイコロを振り始める前の状態)に戻りますので,$(1+E[X])$ を掛けます.
第3項は望みの「2」がでた場合を示しており,「12」と出た上で残りの「3451」がでる期待値を$E[Y_{12}]$ で表しています.
同様の考え方で第3~5式は構成されています.
第6式は賽を振って「2,3,4,5,6」が出た場合には初期状態へと戻り,「1」が出た場合には終了となりますので,このような式となります.
この連立方程式を解きますと
$E[X]=46662, E[Y_{1}]=46656, ... , E[Y_{12345}]=38886$
が得られ,期待値は46662として得られます.
同様に二つ目の問題も連立方程式を立てて考えます.
\[
\left\{
\begin{array}{lcl}
E[X] & = & \frac{5}{6}\left( 1 + E[X]\right) + \frac{1}{6}\left(1+E[Y_{1}]\right) \\
E[Y_{1}] & = & \frac{1}{6}\left(1+E[Y_{1}]\right) + \frac{4}{6}\left( 1 + E[X]\right) + \frac{1}{6}\left(1+E[Y_{12}]\right) \\
E[Y_{12}] & = & \frac{1}{6}\left(1+E[Y_{1}]\right) + \frac{4}{6}\left( 1 + E[X]\right) + \frac{1}{6}\left(1+E[Y_{123}]\right) \\
E[Y_{123}] & = & \frac{1}{6}\left(1+E[Y_{1}]\right) + \frac{4}{6}\left( 1 + E[X]\right) + \frac{1}{6}\left(1+E[Y_{1234}]\right) \\
E[Y_{1234}] & = & \frac{1}{6}\left(1+E[Y_{1}]\right) + \frac{4}{6}\left( 1 + E[X]\right) + \frac{1}{6}\left(1+E[Y_{12345}]\right) \\
E[Y_{12345}] & = & \frac{5}{6}\left( 1 + E[X]\right) + \frac{1}{6} \\
\end{array}
\right.
\]
$E[X]=46872, E[Y_{1}]=46866, ... , E[Y_{12312}]=39060$
積分の計算問題【超難】~問題
\[ \int_0^{\infty} \frac{e^{-tx}(1-\cos x)}{x^2} dx = \frac{\pi}{2} -\arctan t - \frac{t}{2} \log \frac{1+t^2}{t^2} \] を示してください.
積分の計算問題【超難】~解答
与えられた式を示すにあたり,先だって $t > 0$ とき, \[ \int_0^{\infty} \frac{e^{-tx}(1-\cos x)}{x} dx = \frac{1}{2}\log \frac{1+t^2}{t^2} \] を示します. \[ \frac{d}{dt} \frac{e^{-tx}(1 - \cos x)}{x} = -e^{-tx}(1- \cos x) \] に注意すると, \[ \int_0^{\infty} \frac{e^{-tx}(1-\cos x)}{x} dx \\ = \int_0^{\infty} \left( \int_t^{\infty} e^{-xy}(1- \cos x) dy \right) dx \\ = \int_t^{\infty} \left( \int_0^{\infty} e^{-xy}(1- \cos x) dx \right) dy \] となります.ここで,部分積分を用いると \[ \int_0^{\infty} e^{-xy} \cos x dx \\ = \left[ -\frac{1}{y}e^{-xy} \cos x \right]_0^{\infty} - \int_0^{\infty} -\frac{1}{y}e^{-xy} (-\sin x) dx \\ = -\frac{1}{y} - \left[ -\frac{1}{y^2}e^{-xy} \sin x \right]_0^{\infty} + \int_0^{\infty} -\frac{1}{y^2} e^{-xy} (\cos x) dx \\ = \frac{1}{y} - \int_0^{\infty} \frac{1}{y^2} e^{-xy} (\cos x) dx \\ \] となりますから, \[ \left( 1 + \frac{1}{y^2} \right) \int_0^{\infty} e^{-xy} \cos x dx = 1 \] より \[ \int_0^{\infty} e^{-xy} \cos x dx = \frac{y}{1+y^2} \] が得られます.また, \[ \int_0^{\infty} e^{-xy} dx \\ = \left[ -\frac{1}{y} e^{-xy} \right]_0^{\infty} \\ = \frac{1}{y} \] です. 以上のことから, \[ \int_t^{\infty} \left( \int_0^{\infty} e^{-xy}(1- \cos x) dx \right) dy \\ = \int_t^{\infty} \left( \frac{1}{y} - \frac{y}{1+y^2} \right) dy \\ = \left[ \log y - \frac{1}{2} \log (1+y^2) \right]_t^{\infty} \\ = \left[ \frac{1}{2} \log \frac{y^2}{1+y^2} \right]_t^{\infty} \\ = \frac{1}{2} \log \frac{1+t^2}{t^2} \] が得られます.さて, \[ \frac{d}{dt} \frac{e^{-tx}(1 - \cos x)}{x^2} = -\frac{e^{-tx}(1- \cos x)}{x} \] ですから,当初の問題に戻ると, \[ \int_0^{\infty} \frac{e^{-tx}(1-\cos x)}{x^2} dx \\ = \int_0^{\infty} \left( \int_t^{\infty} \frac{e^{-yx}(1- \cos x)}{x} dy \right) dx \\ = \int_t^{\infty} \left( \int_0^{\infty} \frac{e^{-yx}(1- \cos x)}{x} dx \right) dy \\ = \int_t^{\infty} \frac{1}{2} \log \frac{1+y^2}{y^2} dy \\ = \left[ \frac{y}{2} \log \frac{1+y^2}{y^2} +\arctan y \right]_t^{\infty} \\ = \frac{\pi}{2} -\arctan t - \frac{t}{2} \log \frac{1+t^2}{t^2} \] となり,示されました.
